The history of knowledge representation
Introduction
How do systems which process information - either brains or computers - represent that information?
This review draws together many approaches to representating information under the conceptual umbrella of knowledge representation.
Knowledge representation is a very wide and general area of research, approached in an interdisciplinary manner by several different fields. The brain sciences, including psychology, neuroscience and cognitive science, study how the brain represents knowledge. The computer sciences, sometimes influenced by discoveries about the brain, invent ways to encode knowledge digitally. And industry, driven towards what will work or what will be funded, converts these research efforts into larger, working systems which are usually more efficient and correspondingly more restricted.
1. Language
Language, whether it consists of gestures or grammatical utterances, is the oldest and most natural method of knowledge representation available to us.
Sentence parsing
Parsing a sentence means breaking it down into component parts of speech and formalising the relationships between them. What is parsing but generating a knowledge map from a sentence?
There have been various attempts to merge parse trees into larger data structures. Richardson
et al. used a parser and a fixed set of semantic relationships (like hypernym, part, purpose and location) to convert dictionary definitions into graphs like the following:
These approaches have met with limited success, since language is adapted to serialised communication rather than long-term representation of a knowledge base. It can be argued that books are an effective long-term knowledge base - however, they still need to be processed serially. There is no random access to the concepts inside. The index allows occurrences of concepts to be found - but if an idea is not already understood, the reader must start at the beginning in order to be able to follow.
2. Mathematics and logic
Language gives us a natural way to express messages, often with a pragmatic purpose. There has always been a parallel search for a way to express concepts, knowledge, and points of view.

Lewis Carroll's Game of Logic
Kosslyn, Stephen M., William L. Thompson, and Giorgio Ganis. The case for mental imagery. Oxford University Press, 2006.
Mermin, N. D. (2007). Quantum computer science: an introduction. Cambridge University Press.
Formal logic
Formal logic goes back at least to Aristotle, who defined the syllogism, which deduces a conclusion from two premises. Later work added variables, the existential quantifier $$\exists$$ ("something like this is real") and the universal quantifier $$\forall$$ ("this is always true") and the element symbol $$\in$$ ("which belongs to this set"). This allows us to say things like
all dogs are good: $\forall$ dog $\in$ dogs good(dog), or $\forall$ $x$ $\in$ D G($x$)
one dog is the best: $\exists$ dog $\in$ dogs best(dog), or $\exists$ $x$ $\in$ D B($x$).
Before this, statements about existence or universality were difficult to encode:
Stanford Encyclopedia of Philosophy

Here Peirce says that when some $a$ is $b$, it is not the case that all $a$s are not $b$; and when some $a$ is not $b$, it is not the case that all $a$s are $b$.
There are many types of formal logic:
- Aristotelian logic is a primitive logic consisting of terms (like "man" or "mortal"), propositions ("all men are mortal") and syllogisms (inferences which conclude one proposition from two others, the premises).
- Propositional logic or zeroth-order logic allows propositions to be built using logical connectives (and, or, etc). There are no quantifiers or non-logical symbols.
- First-order predicate logic, a key tool for computer science, uses variables and quantifiers and permits non-logical symbols like $man(x)$.
Formal logic can express very complex situations and its constraints make it reasonably computationally tractable. However, like language, it compresses information into a one-dimensional sequence. In a 5-page logical proof, a connection between the first and last pages must use a variable: the connection is not directly expressed in the model. In other words, it is not
iconic.
All men are mortal.
Socrates is a man.
Therefore, Socrates is mortal.
Not much changed - "one of the more remarkable facts of the history of science", according to Kamp & Reyle - until 1879, when Gottlieb Frege published "perhaps the most important single work ever written in logic"
1: (the first incarnation of predicate logic.
Gottlieb Frege, Begriffsschrift (Concept Notation): A formula language of pure thought, modelled upon that of arithmetic, 1879
1. Van Heijenoort in preface to 1970 translation of the above.
Kamp, H., & Reyle, U. (1993). From Discourse to Logic: Introduction to Modeltheoretic Semantics of Natural Language, Formal Logic and Discourse Representation, p. 16
The importance of the Begriffsschrift was not realised for some time, partially due to its complex 2D notation:
This notation, however, has been called "a well thought-out and carefully crafted notation that intentionally exploits the possibilities afforded by the two-dimensional medium of writing like none other." They turn out to be very similar to rotated syntax trees.
Schlimm, D. (2018). On Frege's Begriffsschrift Notation for Propositional Logic: Design Principles and Trade-Offs. History and Philosophy of Logic, 39(1), 53-79.
Frege's later work Grundgesetze (ground-laws) der Arithmetik, was famously torpedoed by Bertrand Russell, who in 1902 discovered a fatal contradiction which Frege was not able to repair.
Coding sentences in formal logic
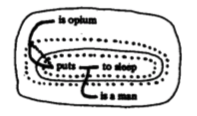
It is difficult to code easy sentences in formal logic. Take "donkey sentences", first analysed by Geach:
"Every farmer who owns a donkey beats it."
"Every police officer who arrested a murderer insulted him."
Peter Geach (1962). Reference and Generality. Ithaca and London: Cornell University Press
These are sentences involving a pronoun whose role, while clear to us, is difficult to define in formal logic.
This turns out to be coded thus in formal logic:

Essentially: for every farmer
x and donkey
y where
x owns
y,
x also beats
y.
Discourse representation theory, proposed in the 1980s by Kamp, deals with this anaphora (long-distance connections between parts of a sentence) by modelling mental representations more closely. Here the donkey sentence is encoded with the help of the variables x (the farmer), y (the donkey), and z (the "it" that is beaten): y and z are also set equal.
Peirce's existential graphs
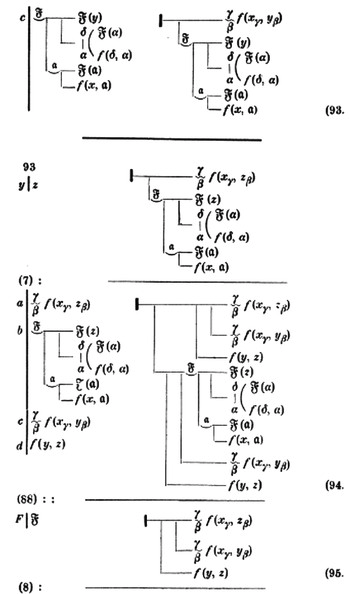
Peirce was one of the first to encode logic using 2D diagrams with his
existential graphs. His early attempts used letters to symbolise logical propositions (here $b$ for
benefactor of and $l$ for
loves) and lines connecting them to symbolise individuals, with a bar meaning "all individuals":
1. Something is at once benefactor and loved of something
2. Something is a lover of itself
3. Everything is a lover of itself
4. Everything is either a lover or a benefactor of everything
His early work was complicated, producing the following diagram encoding "every mother loves some child of hers":
This is quite difficult to understand compared to the English sentence, and is not concise enough to be a useful tool. eventually, inspired by diagrams of chemical bonds, he introduced the relation as a diagrammatic element. This diagram encodes "John gives John to John":
Another innovation was to use shared space to indicate the
or operation. This is how we assert that Rover is a good dog:
We can negate a proposition by giving it a black border ("Rover is not a good dog"):
We encode
or very simply by writing two propositions next to each other on the same surface ("either Rover is a good dog or Larry is a good dog"):
Rover is a good dog
Larry is a good dog
Using just these notations, we can encode implication ("if litmus paper is placed in acid, it will turn red"):
Litmus paper is placed in acid
Litmus paper will turn red
This will be familiar to logicians as "either it turns red, or it hasn't been placed in acid". To encode
and, Peirce makes use of
or and
not. We can write "it's warm and it's sunny" by writing "it's not the case that it's not warm or not sunny":
So far, these statements are universal: there are no relative propositions (which relate to particular individuals or variables). Peirce used the same line introduced earlier to represent both of the two quantifiers. To see which, we look at how the concepts are nested. A line whose least enclosed part is on the outermost level (or inside an even number of circles) means
all ("everything good is ugly"):
A line whose least enclosed part is once enclosed (or inside an odd number of circles) means
some ("something is good and not ugly"):
The system is difficult to understand intuitively, as shown by the following two diagrams:
and not ugly"):
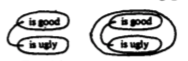
1. Nothing good is ugly
2. Something good is ugly
Peirce called this system
entitative graphs, but soon replaced it with the more complex system of
existential graphs. He extended it by adding further notations called alpha, beta and gamma, including using dotted lines to draw attention to parts of the diagram:
and colours ("tinctures") to express propositional attitudes:
Although Peirce's existential graphs appear rather clumsy and difficult to interpret, but we must view them in the context of his prolific interdisciplinary output and remember that at the time, there were no efficient symbol-processing machines.

Charles Sanders Peirce
1839 - 1914
Roberts, D. D. (2009). The existential graphs of Charles S. Peirce (Vol. 27).
3. Computing and the dawn of artificial intelligence
Peirce's existential graphs were drawn by hand and also processed by hand. Very soon afterwards, machines (programmable or not) took over the job of computation. Computing machines began as special-purpose devices, then became gradually more extensible and programmable. The languages used to program them also became gradually higher-level, more expressive, and closer to natural language. It was, however, some time until computers became fast enough, and programming languages sufficiently high-level, to take on knowledge representation.
Computation
Some time after Ada Lovelace realised that Babbage's Analytical Engine could calculate Bernoulli numbers (widely regarded as the first computer program) and a little after Konrad Zuse built the first programmable computer, it became clear that computers excel not just at representing knowledge but at processing information - generating new knowledge. Much of computer science focusses on resolving problems which are easy to state but difficult to compute, such as sorting or route planning. Cognitive problems such as "how do I work out what John believes" are difficult to state and even harder to compute.
Since the 1950s, a wide range of increasingly high-level programming languages have appeared. Programming began in machine code entered in binary, expressing basic processor instructions by which the programmer was more or less directly responsible for switching electric currents. Machine code grew into a dense tree of higher-level languages, such as C or Fortran (where the programmer is still responsible for managing memory and handling pointers to variables) and later Python or Javascript (where the virtual machine manages memory and deals with pointers).
Should programming languages be considered as part of knowledge representation? The Church-Turing thesis tells us that any language can compute the same things as any other language, but this is not practically true, since an ill-fitting language may take a very long time to compute a problem, and (perhaps more importantly) may take a long time to program. Any knowledge representation system must also of course be programmed in an underlying language.
However, most programming languages are not intended to represent knowledge, but to get stuff done.
Relational databases
The relational paradigm, introduced in the 1960s by British computer scientist Edgar F. Codd, sees the world as tables (relations) which contain rows (records) and columns (attributes). Rows are uniquely identified by certain attributes (keys) and non-key attributes may point to rows in other tables (acting as foreign keys). Although relational databases certainly represent facts, they are not generally considered to do knowledge representation, because their ability to express is so restricted. Information must be encoded in records with rows and columns, and the only way to connect tables is with foreign keys (numbers or strings).
However, the language used to query relational databases, Structured Query Language (SQL) is the only widely-used declarative programming language. Operations such as JOIN (finding matching rows across two tables) and GROUP BY (count or analyse rows after sorting them into different categories, the same operation as Excel pivot tables) are planned out and executed by the SQL server, hiding the details from the programmer. This makes SQL closer to a knowledge representation language than the imperative programming languages, because its primitives are higher-level and clever operations are taking place behind the scenes.
Functional programming: Lisp and its dialects
The most significant bifurcation in the family tree of programming languages was the division into procedural languages (those which directly specify the operations a program should perform, using explicit control flow) and functional languages (which express programs as compositions of functions). Procedural languages directly drive machines and come from thinking about the Turing machine. Functional code requires translation from functions to instructions and comes from thinking about the lambda calculus. The first functional language was Lisp, introduced by McCarthy in 1958.
Lisp and its descendants played a central role in knowledge representation, as functional languages have great expressive power and are highly extensible.
Objects and classes
One of the most popular programming paradigms, object-oriented programming (OOP), allows the programmer to define a class and then to instantiate many objects of that class. These objects all have the same interface and contain the same variables and member functions. OOP is extremely popular because it matches the way we think: human cognition is very good at classifying objects as belonging to a particular class, then assuming that all objects of that class can be used in the same way.
Does OOP constitute knowledge representation? Certainly, the division into objects and classes has been carried forwards by many KR systems, importantly (as we will see later) the semantic web. However, I note that the cognitive division between objects and classes is more complex. In cognition, something can be both a member of a class, and a class; for example, Dog is a member of the class Mammal, but Rover is also a member of the class Dog. Dog is therefore both a member and a class. Cognition can also sometimes consider something as a plain object, and sometimes as a class. It seems therefore that in cognition, classness is a particular way of seeing an object, a particular approach to the object. On the other hand, in object-oriented programming language, something is either an object or not. There may be several levels of class inheritance, but they are all classes - only the lowermost is an object. Objects cannot change class on the fly and we cannot temporarily treat a Dog as a Person, for example, with which human cognition has no problem.
Relational databases
The relational paradigm, introduced in the 1960s by British computer scientist Edgar F. Codd, sees the world as tables (relations) which contain rows (records) and columns (attributes). Rows are uniquely identified by certain attributes (keys) and non-key attributes may point to rows in other tables (acting as foreign keys). Although relational databases certainly represent facts, they are not generally considered to do knowledge representation, because their ability to express is so restricted. Information must be encoded in records with rows and columns, and the only way to connect tables is with foreign keys (numbers or strings).
4. Early work in knowledge representation
We now begin to examine systems which definitely do constitute knowledge representation, starting with linguistics and AI research in the 1950s.
Semantic networks
A semantic network is a graph whose vertices represent concepts and whose edges represent semantic relations. Although early semantic networks were proposed by Alfred Bray Kempe in 1886 and studied by Peirce, they were not further developed until 1956, when they were applied to machine translation in early computational linguistics. The Nude project used semantic networks as an interlingua.
Lehmann, Fritz. Semantic networks in artificial intelligence. Elsevier Science Inc., 1992.
Frames
Frames are a data structure proposed by Minsky which aim to represent stereotyped situations. Frames are basically semantic networks in which nodes contain named "slots" storing particular stereotyped associations.
Slots can be equipped with default values, range restrictions, and type restrictions. Special slots include instance-of (pointing to the node's kind, or superclass).
Frames are closely related with grammar. Slots can play roles similar to the cases of Fillmore's case grammar (Agent, Experiencer, Instrument, Object, Source, Goal, Location, and Time). Fillmore's frame semantics theory of language draws closely on work on frames in AI, and the database FrameNet indexes a large number of frames and their relationships.
Minsky, M. (1974). A framework for representing knowledge.

Marvin Minsky
1927 - 2016
Frames provide a very appealing picture of how a mind might attend to a situation and fill in the blanks. However, they did not prove useful for solving computational problems. I
"Minsky and Schank were trying to express something important, but the actual systems implemented by their students never matched the richness of their original vision. Minsky's wealth of insights dissipated in expert systems where frames became little more than records with pointers to other records... Programmers wrote unmaintainable LISP code to manipulate the data structures."
Sowa, J. F. (1990). Crystallizing theories out of knowledge soup. Intelligent Systems: State of the Art and Future Directions,
Sowa's conceptual graphs
Boxes show concepts and circles represent relations. Here we model the sentence "the cat chased the mouse". The
agent relation links the chase to the cat; the
patient (passive participant) relation links the chase to the mouse. A box represents the entire situation, and is tagged with the
past relation.
Description logics
Semantic networks and frames allow small chunks of knowledge to be expressed and for commonalities to be drawn among different frames (for example, many different frames can include a "location" slot specifying where the action is taking place).
Baader, F., Horrocks, I., Lutz, C., & Sattler, U. (2017). Introduction to description logic. Cambridge University Press.
The "heart" of a description logic is its concept language, "a formal language that allows us to build concept descriptions and role descriptions from concept names, role names, and possibly other primitives". For example,
Description logics place a hard distinction between the properties of the world (which cannot change) and the individual assertions made within that world (which can change). The properties of the world are stored in the Terminology Box (TBox), while any assertions made about objects in the world are stored in the Assertion Box (ABox). This fixed border between the TBox and the ABox mirrors the ability of human cognition to hold some facts constant and view others as changeable; however, human cognition is able to update its world view by learning, and so cognitive distinctions about what is fixed and what is changeable are less set in stone.
| Natural language |
First-order logic |
Description logic |
A teacher is a person who teaches a course.
A student is a person who attends a course.
Students do not teach.
|
∀x (Teacher(x) ⇔ Person(x) ∧ ∃y (teaches(x, y) ∧ Course(y))),
∀x (Student(x) ⇔ Person(x) ∧ ∃y (attends(x, y) ∧ Course(y))),
∀x ((∃y teaches(x, y)) ⇒ ¬Student(x)),
Person(Mary),
Course(CS600), teaches (Mary, CS600).
|
Teacher ≡ Person ⊓ ∃teaches.Course,
Student ≡ Person ⊓ ∃attends.Course,
∃attends.⊤ ⊑ ¬Student,
Mary : Person,
CS600 : Course,
(Mary, CS600) : teaches.
|
Generally, description logics are more expressive than basic propositional logic, but not as expressive as first-order logic, which is undecidable. This limited expressivity means that decision problems in description logics are often decidable, and sometimes even decidable efficiently.
Basic description logics allow more complex concepts to be built up using negation, intersection, and universal restrictions. Extended description logics also allow existential quantification, union, inverse properties, cardinality, and property hierarchies.
5. Mature research and industry projects
There are many mature projects, based either in research or in industry, which aim to represent knowledge. This section reviews several key examples.
WordNet
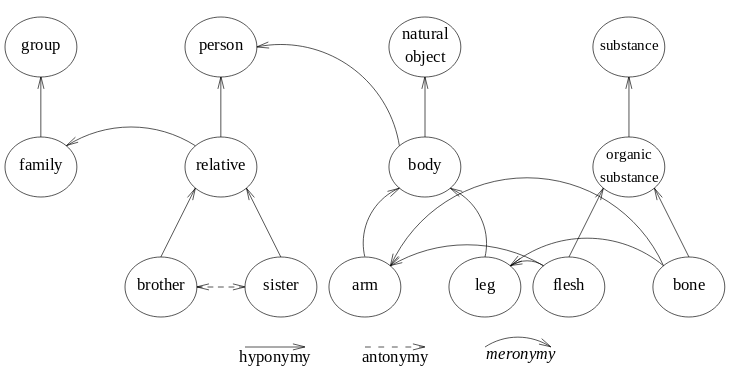
WordNet is a DAG encoding word meaning. The basic object in WordNet is the synset, a group of words expressing the same meaning (synonyms). There can be many words in a synset, and one word can also appear in several synsets if it has different meanings. Synsets are connected by several conceptual relationships, first for nouns:
- Hypernyms and hyponyms: inheritance (canine is a hypernym of dog, dog is a hyponym of canine)
- Coordinate terms: siblings (dog and wolf are coordinate terms as they share the hypernym canine). This also works for verbs.
- Meronyms and holonyms: part-whole relationship (window is a meronym of building, building is a holonym of window)
and then for verbs:
- Hypernyms and troponyms: inheritance (to perceive is an hypernym of to listen, to lisp is a troponym of to talk)
Synsets are also equipped with English definitions and examples of use.
- Entailment: if you are doing X you must be doing Y (to sleep is entailed by to snore)
Cyc
Cyc (from "encyclopedia") is one of the largest semantic knowledge bases. In the words of creator Douglas Lenat, it is "a universal schema of roughly $10^5$ general concepts spanning human reality." Started in 1984, the knowledge base was hand-crafted by "a person-century of effort". Equipped with an inference engine, Cyc aims to keep the number of facts explicitly encoded in its database to a minimum and use an inference engine to work out as many as it can.
Lenat, D. B. (1995). CYC: A large-scale investment in knowledge infrastructure. Communications of the ACM
A major challenge for Cyc was context: most facts are not always true, but are only true in a certain context. In some contexts, certain facts may not make sense at all (which way is up in space?). This means that
Cyc handles this by modelling context explicitly.
Cyc was always very ambitious. In 1989, Lenat and Guha claimed that by 1999, "no one would even think of buying a computer that doesn't have Cyc running on it". John F. Sowa's students, on learning about Cyc, "would have preferred a less ambitious system they could use immediately to a grandiose system that might solve all the problems of AI at some indefinite time in the future."
Sowa, J. F. (1993). Book review: Building large knowledge-based systems: Representation and inference in the cyc project by DB Lenat and RV Guha.
Goodfellow, I., Bengio, Y., Courville, A., & Bengio, Y. (2016). Deep learning (Vol. 1, No. 2). Cambridge: MIT press.
An example of how Cyc can fail is given by Goodfellow et al:
"Cyc failed to understand a story about a person named Fred shaving in the morning... Its inference engine detected an inconsistency in the story: it knew people do not have electrical parts, but because Fred was holding an electric razor, it believed the entity 'FredWhileShaving' contained electrical parts. It therefore asked whether Fred was still a person while shaving."
KnowItAll
Automatically extracting information from Web pages has always been tempting. In 2004, the University of Washington's KnowItAll project uses sentence parsing and hand-engineered rules to extract information from web pages and from specific search queries it makes itself. This rule extracts a country name from a sentence like "China is a country in Asia" as long as "country" is not the head of a noun phrase (to prevent matching "Garth Brooks is a country singer" where it is used as an adjective):
This rule finds instances of athletes playing for a particular sports team:
KnowItAll required manual rule crafting and was backed by an RDBMS, which made it difficult to extend. A conclusive analysis of its precision was not conducted.
Etzioni, O., Cafarella, M., Downey, D., Kok, S., Popescu, A. M., Shaked, T., ... & Yates, A. (2004, May). Web-scale information extraction in KnowItAll: (preliminary results). In Proceedings of the 13th international conference on World Wide Web (pp. 100-110).
Freebase
Freebase, started in 2007 by software company Metaweb, was another large collection of collaboratively edited structured data. It used a graph data structure consisting of nodes and links, backed by a triplestore and accessible with the MQL query language.
Freebase enventually grew to 44 million topics and 2.4 billion facts. Its "folksonomy" approach allowed overlapping and contradictory assertions. However, Metaweb employees were responsible for approving user-entered facts, and users were not able to edit each others' facts. In 2010, Metaweb was acquired by Google and Freebase was incorporated into an early version of the Google Knowledge Graph. Google eventually shut down Freebase in 2015.
YAGO
YAGO (Yet Another Great Ontology) is an open-source knowledge base automatically derived from Wikipedia and WordNet by a research group at Germany's Max Planck Institute. A page on Wikipedia maps onto an entity in YAGO. It contains more than 1.7 million entities and 15 million facts and its precision has been shown to be around 95% thanks to the use of type checking techniques. It includes a natural way to represent $n$-ary relations.
Suchanek, F. M., Kasneci, G., & Weikum, G. (2008). Yago: A large ontology from Wikipedia and Wordnet. Journal of Web Semantics.
6. The semantic web
The early Internet drove the development of HTML (Hypertext Markup Language), a language designed to author and transmit web pages. The term "semantic web", coined by Tim Berners-Lee, refers to the augmentation of markup files with semantic information that expresses facts about the concepts detailed on a web page, not just markup information controlling how the page should be displayed.
Today, the Semantic Web is a collection of approaches to knowledge representation and reasoning which, under the guidance of industry, have become specialised for a single application: encoding semantic information into web pages and allowing them to communicate.
RDF: Resource Description Framework
The
Resource Description Framework (RDF) is a specification for a data model for the semantic web. The semantic web uses an ontological approach: in this context, an ontology is a formalised taxonomy defining what kind of objects can be modelled (nouns) and what kind of relationships can exist between them (verbs). Once an ontology has been defined, it can be used in semantic web documents and services.
The other meaning of ontology is a branch of metaphysics concerned with the nature and
relations of being.
The RDF Schema (RDFS) is a commonly-used schema language which describes classes of objects operating within the RDF specification. RDFS can be concisely expressed using the Turtle format; here we say that David and Lee are people and that Lee admires David, all within the
csi context.
csipeople:David
rdf:type foaf:Person;
rdfs:label “David Tester”;
csi:people:Lee
rdf:type csi:MyNewPersonClass;
csi:admires csipeople:David.
www.cambridgesemantics.com/blog/semantic-university/learn-owl-rdfs/
RDF knowledge bases can be queried with the SPARQL query language. The following query asks "what are all the country capitals in Africa?". The variables
?capital and
?country will return the results.
SPARQL is a recursive acronym for SPARQL Protocol and RDF Query Language.
https://en.wikipedia.org/wiki/SPARQL
Ontologies are defined using a family of knowledge representation languages known as OWL (Web Ontology Language). The following ontology states that animals eat things, people are animals, men are people who are male and adult, and animal lovers are people who have at least 3 pets.
Class(pp:animal partial
restriction(pp:eats someValuesFrom(owl:Thing)))
Class(pp:person partial pp:animal)
Class(pp:man complete
intersectionOf(pp:person pp:male pp:adult))
Class(pp:animal+lover complete
intersectionOf(pp:person
restriction(pp:has_pet minCardinality(3))))
We can add the "eats" and "eaten by" relationships (which are each other's inverse) and specify their domains and ranges (what their subjects and objects can be):
ObjectProperty(pp:eaten_by)
ObjectProperty(pp:eats inverseOf(pp:eaten_by)
domain(pp:animal))
ObjectProperty(pp:has_pet domain(pp:person)
range(pp:animal))
OWL reasoners can then make the appropriate deductions: if an entity appears which is a male adult person with 4 pets, the system can conclude that this entity is a man and an animal lover. There is of course a tradeoff in the expressivity of the language:
- OWL Lite has fast and easy reasoning but limited expressivity.
- Owl DL, like OWL Lite, uses a description logic and is still decidable (reasoning computations are guaranteed to terminate).
- OWL Full uses a different semantics based on RDFS. It supports additional features such as allowing classes to be treated as objects; however, it is unfortunately undecidable.
The core of RDF is a
statement, connecting two resources (the subject and object) using a predicate.
www.cs.man.ac.uk/~horrocks/ISWC2003/Tutorial/
Semantic web approaches to reasoning have found limited utility in cognitive science due to their specialisation for web applications (for example their reliance on URLs) and the intractability of complex reasoning in OWL Full. However, their languages, especially OWL and Turtle, have now become a lingua franca for interchanging semantic information online.
DBpedia
The DBpedia project aims to extract multilingual knowledge from Wikipedia and structure it using Semantic Web technologies. It extracts information mainly from Wikipedia infoboxes, which are already structured and highly accurate. The English edition contains 400 million facts describing 3.7 million things. Its multilingual ontology contains 320 classes and 1,650 properties. The knowledge base is updated when Wikipedia changes and queries can be made in SPARQL.

Wikipedia infobox for the common blackbird
Lehmann, J., Isele, R., Jakob, M., Jentzsch, A., Kontokostas, D., Mendes, P. N., ... & Bizer, C. (2015). Dbpedia–a large-scale, multilingual knowledge base extracted from wikipedia. Semantic web, 6(2), 167-195.
As with YAGO, an entity on Wikipedia becomes and entity in DBpedia. The syste uses custom parsing to turn a Wikipedia page into an abstract syntax tree, then traverse it to extract facts and save them to a triplestore, Virtuoso, where they can be seen through web browsers, RDF browsers, or SPARQL queries. In a Wikpedia page, an infobox is stored like this:
{{Infobox automobile
| name = Ford GT40
| manufacturer = [[Ford Advanced Vehicles]]
| production = 1964-1969
| engine = 4181cc
(...)
}}
The data extracted by DBpedia could look like this:
dbr:Ford_GT40
dbp:name "Ford GT40"@en;
dbp:manufacturer dbr:Ford_Advanced_Vehicles;
dbp:engine 4181;
dbp:prod
Typing is done heuristically - an engine size could end up as an integer or could be expressed in the article as a string (cc4181).
DBpedia has become a central hub for the Linked Open Data (LOD) cloud:
https://www.cambridgesemantics.com/blog/semantic-university/intro-semantic-web/intro-linked-data/
DBpedia deals with different languages by producing a localised data set for each one, plus a canonicalised data set for each language in which entities are linked to their pages in the English Wikipedia. The localised datasets contain more information as there is much which cannot be canonicalised. The DBpedia ontology is multilingual:

According to Lehmann
et al.,
"One of the main differences between DBpedia and YAGO in general is that DBpedia tries to stay very close to Wikipedia and provide an RDF version of its content. YAGO focuses on extracting a smaller number of relations compared to DBpedia to achieve very high precision and consistent knowledge. The two knowledge bases offer different type systems: whereas the DBpedia ontology is manually maintained, YAGO is backed by WordNet and Wikipedia leaf categories. Due to this, YAGO contains many more classes than DBpedia."
Inference engines
Many of the systems we have seen go beyond their original goal of representing knowledge and aim to do more: to infer, to deduct and to answer questions.
7. Problems with existing approaches to knowledge representation
Knowledge representation is nowhere near a solved problem. In contrast to this fact there stand the many knowledge representation researchers who have confidently predicted that the problem was nearly solved. The young Leibniz, suggesting his universal language of thought and its reasoning engine, wrote that
"If controversies were to arise, there would be no more need of disputation between two philosophers than between two calculators. For it would suffice for them to take their pencils in their hands and to sit down at the abacus, and say to each other (and if they so wish also to a friend called to help): Let us calculate."
and, more recently, Tim Berners-Lee hoped in 1999 that the Semantic Web would
"become capable of analyzing all the data on the Web – the content, links, and transactions between people and computers. ...when it does, the day-to-day mechanisms of trade, bureaucracy and our daily lives will be handled by machines talking to machines. The "intelligent agents" people have touted for ages will finally materialize."
Earlier, we saw that Lenat and Guha claimed that Cyc would by 1999 be installed on every personal computer. These examples suggest that knowledge representation has a tendency to seem an easier problem than it actually is. One reason for this could be that, cognitively, knowledge representation appears easy because much of it is unconscious. Moravec's paradox points this out, reminding us that reasoning is computationally easy compared to perception.
The inconsistency of human thought
Building a large knowledge base requires bringing together disparate facts. It is not guaranteed that facts from different worldviews, mindsets or approaches will work well together, can be expressed in the same formalism, or will be free from inconsistencies and contradictions.
Sowa summed up this view:
"that the total knowledge in a person's head is too large and too disorganized to be called a knowledge base. Instead, it consists of many chunks of knowledge, each of which is internally consistent, but possibly inconsistent with one another. The metaphor of knowledge soup more
accurately conveys the highly fluid, loosely organized, and rapidly changing state of human knowledge."
and so:
"no ontology can ever be complete and perfect for all time"
Sowa, J. F. (1990). Crystallizing theories out of knowledge soup. Intelligent Systems: State of the Art and Future Directions,
The Semantic Web technologies mainly address research-oriented problems: finding the capitals of countries, the stars of films, and so forth. This kind of problem has extensive application and have been very useful for building web services. However, it is a completely different kind of problem from those approach by neuroscience and AGI: how does an agent solve a particular task which is in front of it, taking into account its perceptions and memories?
Knowledge bases are repositories of facts, but facts cannot all be represented at once and encoding them without context is difficult. They do not have episodic memories,
Learning curves and ease of use
Many of the knowledge representation systems we have just reviewed are difficult to adopt without a significant amount of specialist training. There are many potential use cases for simple and flexible knowledge representation systems. For example, a philosopher may want to describe a simple scenario - but semantic web tools require difficult installation and configuration and learning a good deal of unfamiliar syntax.
8. Conclusions